Kostenfunktion

3.4.1 Durchschnitts- und Grenzkosten

Betriebsminimum, -optimum

ie Ermittlung von Durchschnitts- und Grenzkosten unterscheidet sich technisch nicht von der Ermittlung von Durchschnitts- und Grenzerträgen. Durchschnitts- oder Stückkosten wurden bereits mehrfach, so z.B. im einführenden Dinger-Beispiel, betrachtet. Sie zeigen genau das an, was ihr Name sagt: die Kosten pro Stück.

Mit Durchschnittskosten sind immer die totalen durchschnittlichen Kosten gemeint. Werden die variablen Kosten pro Ausbringungseinheit berechnet, spricht man von durchschnittlichen variablen Kosten. Da sich die gesamten Kosten ($C$) aus variablen ($VC$) und fixen Kosten ($F$)

$$ C = F + VC \tag{1} $$

ergeben, gilt natürlich, dass die durchschnittlichen totalen Kosten ($DTK$) in durchschnittliche variable ($DVK$) und durchschnittliche fixe Kosten ($DFK$) aufgespalten werden können:

$$ DTK = DFK + DVK \tag{2} $$

Zweifelsohne spielen die Stückkosten eine wichtige Rolle bei der Angebotsplanung der Unternehmung. Entscheidender sind allerdings die sogenannten Grenzkosten.

Eigentlich müsste man etwas neutraler formulieren, um welchen Betrag sich die Kosten "verändern", denn rein theoretisch könnten die Kosten mit steigender Produktion ja auch sinken. Das ist aber äußerst unwahrscheinlich (regressiver Kostenverlauf).

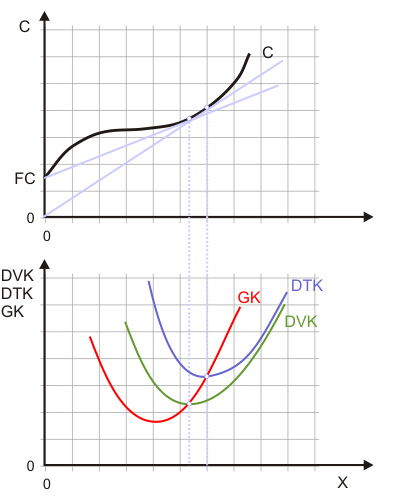
In Abbildung 1 ist ein ertragsgesetzlicher (kurzfristiger) Kostenverlauf angenommen. Mit dem bereits mehrfach eingesetzten grafischen Instrumentarium wird im unteren Diagramm der Verlauf der Stückkosten, der durchschnittlichen variablen Kosten und der Grenzkosten dargestellt. Dass die Grenzkostenkurve die Kurven der durchschnittlichen totalen und durchschnittlichen variablen Kosten jeweils in deren Minima schneidet, ist vollkommen analog zum ausführlich betrachteten Zusammenhang zwischen Grenz- und Durchschnittsertrag zu sehen. Eine maßstabsgetreue Darstellung für ein Zahlenbeispiel zum klassischen Kostenverlauf findet sich am Ende dieses Abschnitts.

Im Zusammenhang mit der an späterer Stelle zu erörternden Produzentenrente wird von Bedeutung sein, dass die Fläche unter der Grenzkostenfunktion den variablen Kosten entspricht. An einem simplen Zahlenbeispiel soll dies verdeutlicht werden. Unterstellt sei eine lineare Kostenfunktion:

$$ C = 2 + 5x \tag{3}$$

Die Grenzkosten sindhier konstant 5 - die Grenzkostenfunktion ist also eine Parallele zur Abszisse. Die Fläche unter der Grenzkostenfunktion ist gleich den variablen Kosten: Betrachten wir das z.B. für $x = 10$. Dann ist die Fläche unter der Grenzkostenfunktion 10 mal 5, also gleich 50. Diesen Wert liefert die Kostenfunktion (3) aber auch für die variablen Kosten.

Da die Grenzkostenfunktion ($GK$) die erste Ableitung der Kostenfunktion ($C$) ist, entspricht die Fläche unter der Grenzkostenfunktion der Stammfunktion von $C$. Das sind aber gerade die variablen Kosten:

$$ C(x) = VC(x) +F \tag{4} $$ $$ GK = \cfrac{\text{d}C(x)}{\text{d}x} \tag{5}$$ $$ \int_0^{x_0} GK \text{d}x = VC(x_0) \tag{6} $$

Die maßstabsgetreue Grafik zum Zahlenbeispiel, das im letzten Absatz dieser Seite verlinkt ist, lässt dies für einen klassischen Kostenverlauf erkennen.

Wenn man Grenz- und Durchschnittskostenverläufe für eine neoklassische Produktionsfunktion darstellt, findet man nicht "so schöne" u-förmige Kurven wie im klassischen Fall. Abbildung 2 ist konstruiert anhand des Zahlenbeispiels

$$ C = 10.000+2x+0,1x^2 \tag{7} $$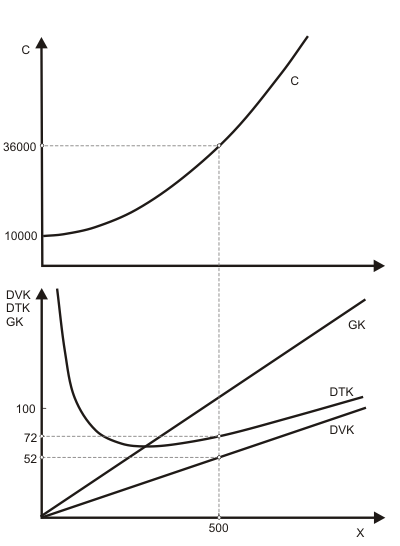

Für das oben angesprochene Zahlenbeispiel (maßstabsgetreue Grafik) zum ertragsgesetzlichen Kostenverlauf ist im Vorgriff auf die Erklärung der Angebotsfunktion bereits die gewinnmaximierende Ausbringungsmenge bestimmt. Der Zusammenhang zwischen den Flächen unter der Grenzkostenfunktion und den variablen Kosten gilt aber natürlich für jede beliebige Produktionsmenge.